Here’s a Quick Way to Connect RS232 Equipment
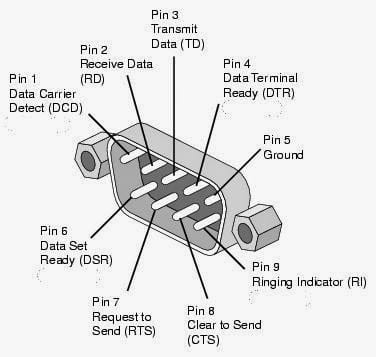
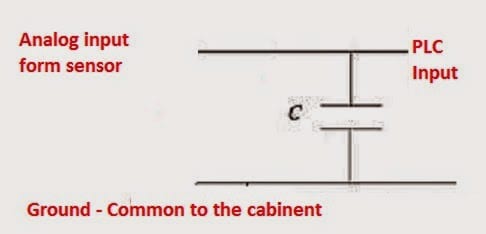
Most programmable controllers will come with an RS232 communication port. This recommended standard (RS) has voltage signals between 3 to 15 volts DC concerning the ground/common pin. RS232 devices are called DTE (data terminal equipment) or DCE (data communication equipment). The maximum cable length for the communication cable is 15m; however, depending on the environment, … Read more