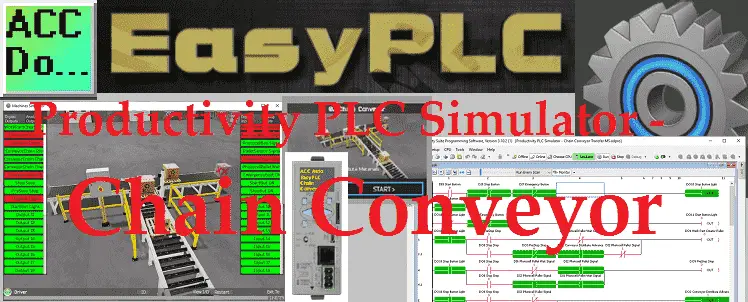
Productivity PLC Simulator – Chain Conveyor MS
The Machine Simulator (MS) is part of the EasyPLC software suite. It has many built-in machines that can be programmed. The chain conveyor is one of these machines. It will transfer large and small boxes on the line to different locations. The productivity series of PLCs will be used to program this virtual machine. Using … Read more